publications
journal papers, conference papers & drafts, patents, and theses
journal papers
2025
2024
2023
2022
2021
2018
conference papers & drafts
2021
2019
-
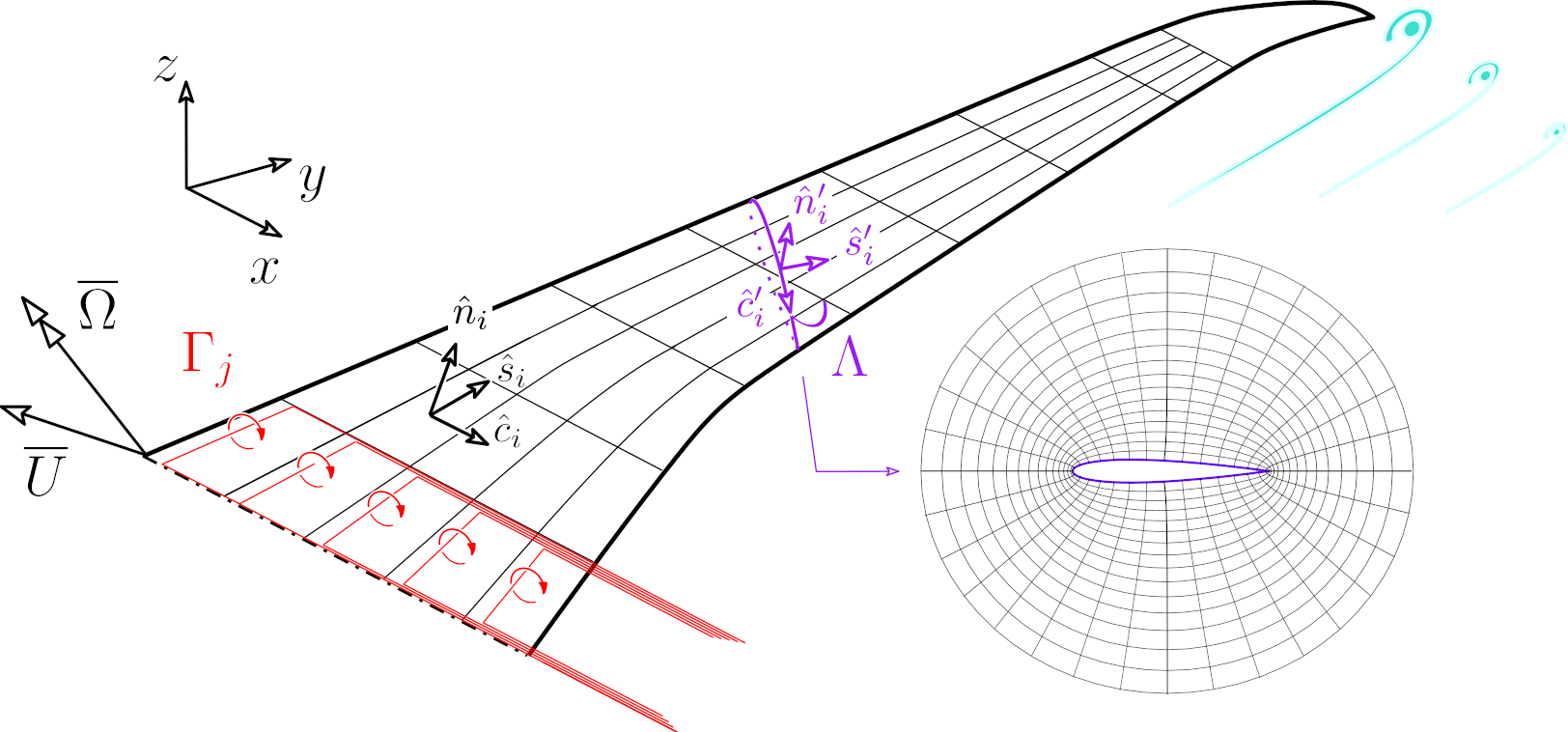
 Viscous-inviscid analysis of transonic swept wings using 2.5D RANS and parametric shapesIn AIAA Scitech 2019 Forum, Jan 2019
Viscous-inviscid analysis of transonic swept wings using 2.5D RANS and parametric shapesIn AIAA Scitech 2019 Forum, Jan 2019
2018
- An extended rough-wall model for an integral boundary layer model intended for ice accretion calculationsIn 10th AIAA Atmospheric and Space Environments Conf., Jan 2018
2017
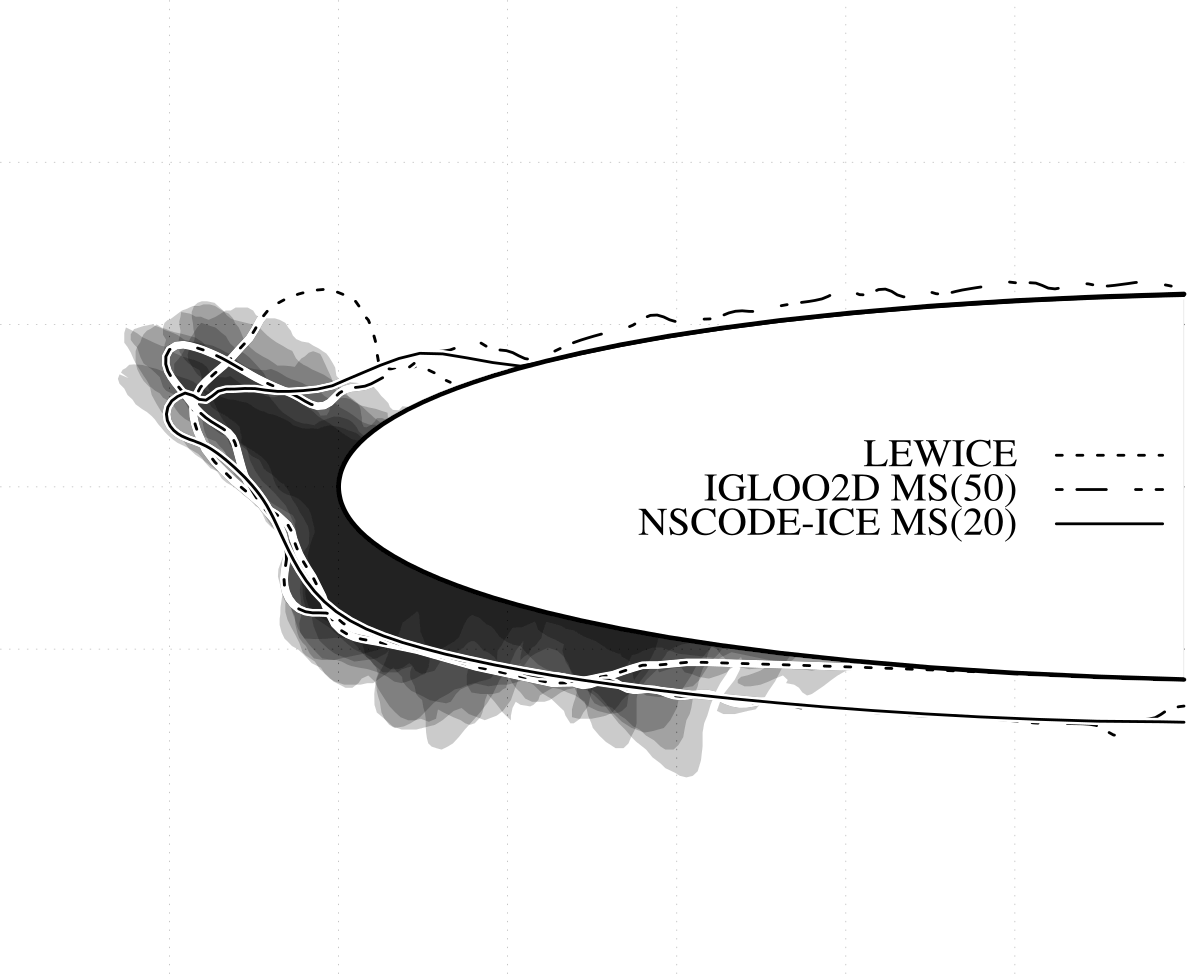
- Description and assessment of the new ONERA 2D icing suite IGLOO2DIn 9th AIAA Atmospheric and Space Environments Conf., Jan 2017
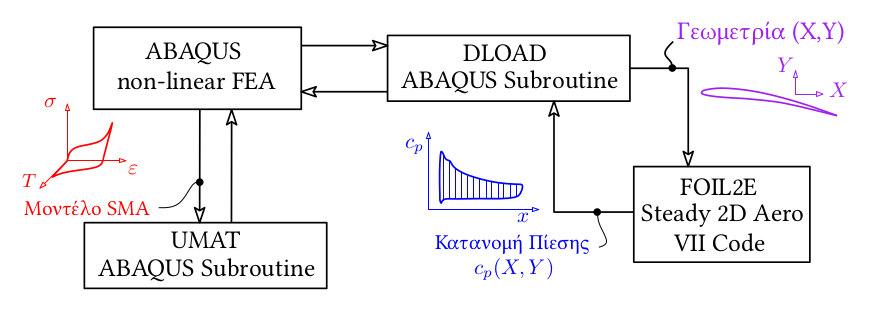
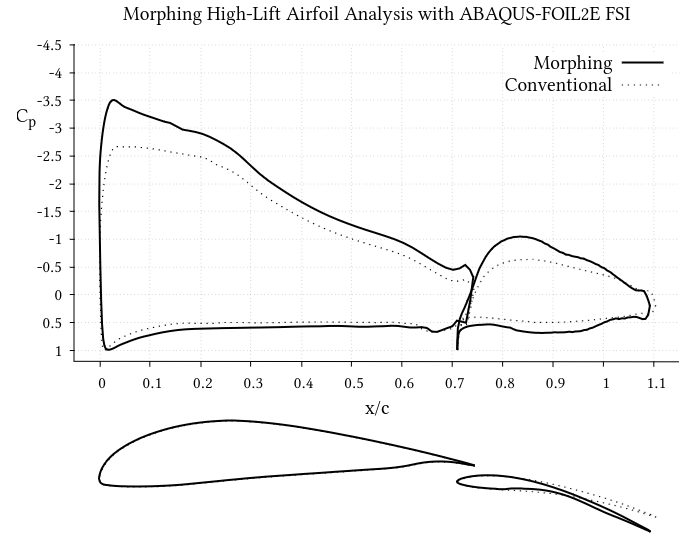
- A robust fluid-structure interaction numerical tool for the analysis of airfoil morphing structures with shape memory alloy actuatorsIn VIII ECCOMAS Thematic Conf. on Smart Structures and Materials (SMART), Jan 2017
patent
2022
-
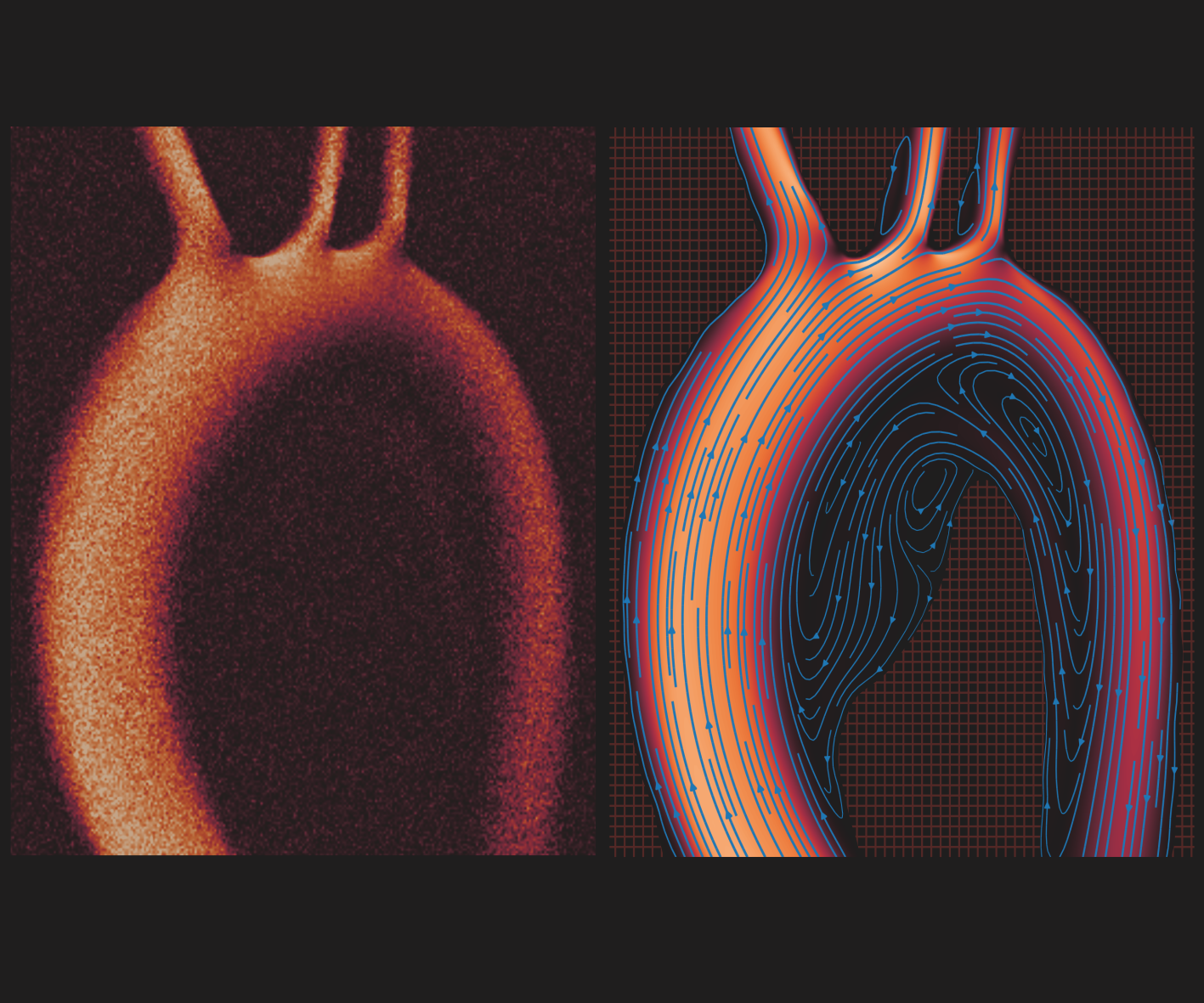
 Methods and systems for improved reconstruction of magnetic resonance velocimetry data and a method of compressing flow data of a fluid2022
Methods and systems for improved reconstruction of magnetic resonance velocimetry data and a method of compressing flow data of a fluid2022